Οι αρχαίοι Έλληνες δεν έδωσαν λύσεις βιώσιμες στο πρόβλημα παράστασης των φυσικών αριθμών. Χρησιμοποίησαν για την παράσταση των αριθμών το αλφάβητό τους.

Οι αρχαίοι Έλληνες ήταν απίστευτα ταλαντούχοι μαθηματικοί, αλλά σπάνια χρησιμοποιούσαν αριθμούς στα μαθηματικά τους.  Ακόμη και ο Πυθαγόρας, ενδιαφερόταν πολύ περισσότερο για τα διαγράμματα παρά για συγκεκριμένες καταστάσεις.

Αλλά οι αρχαίοι Έλληνες είχαν σίγουρα αριθμούς. Στην πραγματικότητα, είχαν αυτό που ήταν κατά κάποιο τρόπο ένα πολύ πιο καλο σύστημα από τους βαρετούς ρωμαϊκούς αριθμούς, όπως I, II, III που εξακολουθούμε να υιοθετούμε περιστασιακά σήμερα. Όπως και οι λατινικοί αριθμοί, το σύστημά τους δανειζόταν γράμματα. Όπως και οι αραβικοί αριθμοί που χρησιμοποιούνται ακόμα, χρειαζόταν μόνο ένα σύμβολο για κάθε δεκαδικό ψηφίο.

Τον 6ο αιώνα π.Χ., το ελληνικό αλφάβητο χρησιμοποιούσε 24 γράμματα. Για να φτιάξουν αριθμούς, οι Έλληνες πρόσθεσαν τρία ακόμη σύμβολα (οι λογαριασμοί διαφέρουν ως προς το αν αυτά ήταν παλαιότερα γράμματα ή νέοι χαρακτήρες), στη συνέχεια τα έβγαλαν εννέα τη φορά για να προσδιορίσουν τις στήλες των μονάδων, των δεκάδων και των εκατοντάδων. Ως εκ τούτου:

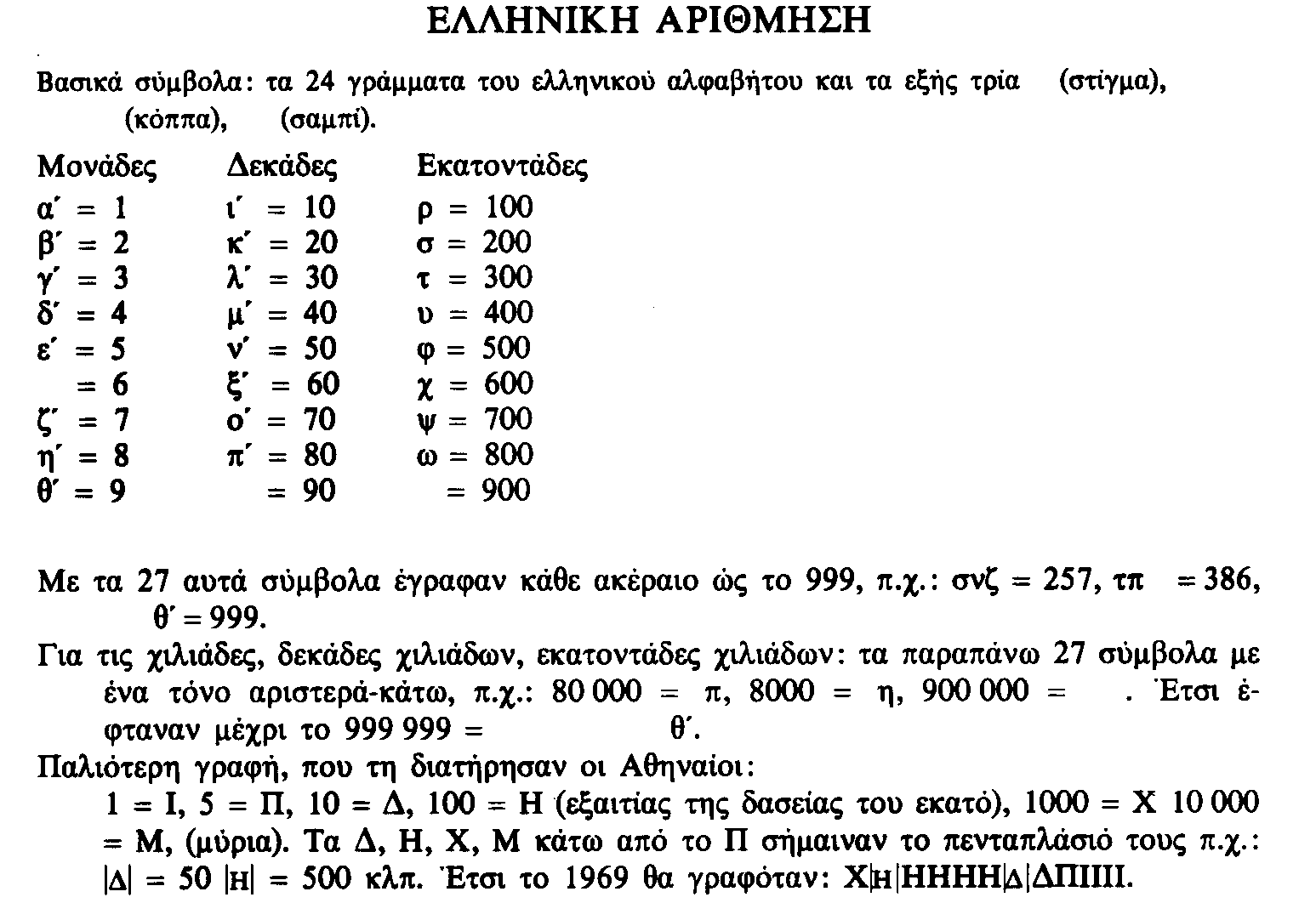
Για το πενταπλάσιο ενός αριθμού χρησιμοποιούσαν το σύμβολο του αριθμού κάτω από το Π : έτσι το Π , Π σήμαινε αντίστοιχα 5*1000 ,5*10. Για το 1 χρησιμοποιούσαν το σύμβολο Ι. Η παράσταση των αριθμών γινόταν με τα γράμματα του τότε αλφαβήτου και με τη χρησιμοποίηση της θέσης του καθενός τους στο αλφάβητο ως εξής :τα α, β, γ, δ, ε, s (στίγμα),ζ, η, θ για τους 1, 2, 3, 4, 5, 6, 7, 8, 9 (μονάδες) , τα ι,κ,λ,μ,ν,ξ,ο,π,7 (“κόππα”) για τους 10, 20, 30, 40, 50, 60, 70, 80, 90 (δεκάδες), τα ρ, σ, τα, υ, φ, χ, ψ, ω, (“σαμπί”) για τους 100, 200, 300, 400, 500, 600, 700, 800, 900 (εκατοντάδες). Κατά την γραφή αυτή ια, ιβ, κγ, ρα κ.λ.π., σήμαιναν αντίστοιχα: 10+1 (=11), 10+2 (=12), 20+3 (=23), 100+1 (=101) κ.λ.π. Το πρόβλημα με αυτό το αριθμητικό σύστημα ήταν ότι δεν ήταν δυνατή η παράσταση μεγάλων αριθμών με έναν περιορισμένο αριθμό συμβόλων.

Πραγματικά εξέχουσες ανακαλύψεις στα μαθηματικά ήταν αυτές που έγιναν από τον Πυθαγόρα και τους μαθητές του. Αφορούσαν όχι μόνο τους περιττούς και άρτιους ή τους απλούς και σύνθετους αριθμούς, αλλά τους απλούς αριθμούς που αναφέρονται σε σχήματα, δηλαδή σε αριθμούς που επινοήθηκαν για να παραστήσουν τα σημεία ενός επίπεδου σχήματος ή ενός τρισδιάστατου σχήματος. Διατύπωσαν τη θεωρία των αναλογιών, καθώς και τη θεωρία της αναλογίας των μουσικών διαστημάτων προς το μήκος μιας χορδής σταθερά τεντωμένης. Η Πυθαγόρεια αριθμητική περιλαμβάνει τη θεωρεία των “πλευρικών”, “διαμετρικών” και “τέλειων” αριθμών και ήταν η πρώτη θεωρεία που καθόρισε τους ασύμμετρους και τους ασύμφωνους αριθμούς.

Όλα μαζί, έφτασαν έναν Έλληνα στα 99.999.999, ενας αριθμός πολύ μεγαλύτερος από ό,τι χρειαζόταν ποτέ, είτε για την καθημερινή ζωή είτε για πολύπλοκα μαθηματικά. Μπορούσαν επίσης να χωρέσουν κλάσματα: Ένα σημάδι στην επάνω δεξιά γωνία ενός αριθμού σήμαινε ένα διαιρούμενο με αυτόν τον αριθμό και ανέπτυξαν ειδικά σύμβολα για κοινά κλάσματα όπως το 1/2.

Αυτό το αλφαβητικό σύστημα μέτρησης πρωτοεμφανίστηκε ως τοπικό φαινόμενο στα ελληνικά νησιά του Αιγαίου κατά τον 6ο αιώνα π.Χ., πιθανότατα υιοθετήθηκε από τους Αιγύπτιους μέσω του εμπορίου. Την ίδια περίπου εποχή, ο Πυθαγόρας έφερε επανάσταση στα μαθηματικά με το θεώρημά του λίγα μόλις νησιά μακριά, στη Σάμο (αν και δεν έχουμε καμία σαφή απόδειξη ότι χρησιμοποιούσε αλφαβητικούς αριθμούς). 

Ακόμη και σε τοπικό επίπεδο, οι αλφαβητικοί αριθμοί έπεσαν από τη δημοτικότητά τους για περίπου 150 χρόνια, μόνο για να επανέλθουν βιαστικά στη σκηνή στα τέλη του 4ου αιώνα π.Χ., ακριβώς στην ώρα που ο Αρχιμήδης ανακάλυψε τη χαρά των εφαρμοσμένων μαθηματικών και ο Πτολεμαίος υπολόγισε το γεωγραφικό πλάτος χιλιάδων των τόπων.